Modeling the Performance of Early Fault-Tolerant Quantum Algorithms

Abstract

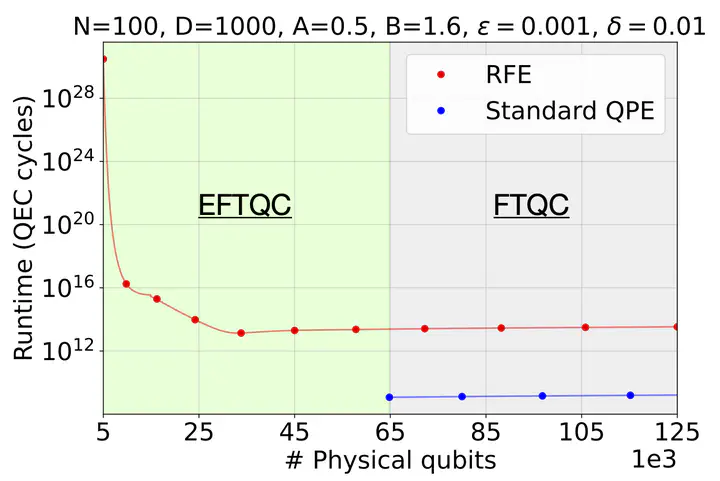
Progress in fault-tolerant quantum computation (FTQC) has driven the pursuit of practical applications with early fault-tolerant quantum computers (EFTQC). These devices, limited in their qubit counts and fault-tolerance capabilities, require algorithms that can accommodate some degrees of error, which are known as EFTQC algorithms. To predict the onset of early quantum advantage, a comprehensive methodology is needed to develop and analyze EFTQC algorithms, drawing insights from both the methodologies of noisy intermediate-scale quantum (NISQ) and traditional FTQC. To address this need, we propose such a methodology for modeling algorithm performance on EFTQC devices under varying degrees of error. As a case study, we apply our methodology to analyze the performance of Randomized Fourier Estimation (RFE), an EFTQC algorithm for phase estimation. We investigate the runtime performance and the fault-tolerant overhead of RFE in comparison to the traditional quantum phase estimation algorithm. Our analysis reveals that RFE achieves significant savings in physical qubit counts while having a much higher runtime upper bound. We anticipate even greater physical qubit savings when considering more realistic assumptions about the performance of EFTQC devices. By providing insights into the performance trade-offs and resource requirements of EFTQC algorithms, our work contributes to the development of practical and efficient quantum computing solutions on the path to quantum advantage.

Qiyao (Catherine) Liang

PhD student at MIT EECS

I’m a third-year PhD student in the Electrical Engineering and Computer Science department at MIT. My primary interest is in the intersection of physics, AI, and neuroscience. I’m advised by Ila Fiete from the MIT Brain and Cognitive Science department. Some of my recent interests are understanding the mechanisms of compositional generalization in generative models, how structural and/or functional modularity emerge within artificial and biological systems, and beyond. I’m interested in a broad range of topics regarding studying the principles of artificial/biological intelligence and consciousness as emergent phenomena, via quantitative tools from physics as well as empirical studies. I completed my undergraduate studies at Duke University in physics and math, where I worked on controlling and denoising quantum computers.