Compositional Generalization via Forced Rendering of Disentangled Latents

Abstract

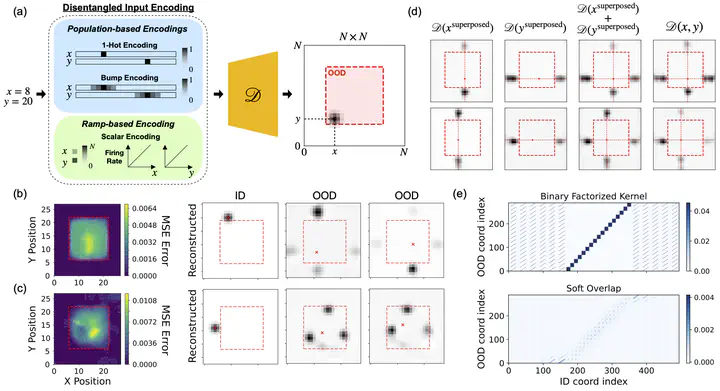
Composition—the ability to generate myriad variations from finite means—is believed to underlie powerful generalization. However, compositional generalization remains a key challenge for deep learning. A widely held assumption is that learning disentangled (factorized) representations naturally supports this kind of extrapolation. Yet, empirical results are mixed, with many generative models failing to recognize and compose factors to generate out-of-distribution (OOD) samples. In this work, we investigate a controlled 2D Gaussian bump generation task with fully disentangled (x,y) inputs, demonstrating that standard generative architectures still fail in OOD regions when training with partial data, by re-entangling latent representations in subsequent layers. By examining the models learned kernels and manifold geometry, we show that this failure reflects a memorization strategy for generation via data superposition rather than via composition of the true factorized features. We show that when models are forced—through architectural modifications with regularization or curated training data—to render the disentangled latents into the full-dimensional representational (pixel) space, they can be highly data-efficient and effective at composing in OOD regions. These findings underscore that disentangled latents in an abstract representation are insufficient and show that if models can represent disentangled factors directly in the output representational space, it can achieve robust compositional generalization.

Qiyao (Catherine) Liang

PhD student at MIT EECS

I’m a third-year PhD student in the Electrical Engineering and Computer Science department at MIT. My primary interest is in the intersection of physics, AI, and neuroscience. I’m advised by Ila Fiete from the MIT Brain and Cognitive Science department. Some of my recent interests are understanding the mechanisms of compositional generalization in generative models, how structural and/or functional modularity emerge within artificial and biological systems, and beyond. I’m interested in a broad range of topics regarding studying the principles of artificial/biological intelligence and consciousness as emergent phenomena, via quantitative tools from physics as well as empirical studies. I completed my undergraduate studies at Duke University in physics and math, where I worked on controlling and denoising quantum computers.